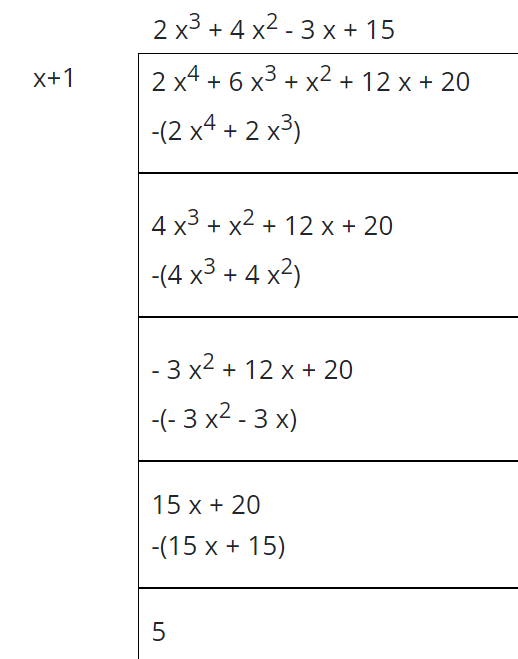To calculate result you have to disable your ad blocker first.
Division De Polinomios Calculadora
Para encontrar la división larga del polinomio, ingrese el numerador y el denominador del polinomio y haga clic en el botón calcular usando la calculadora de división larga del polinomio.
Calculadora De Division De Polinomios
La calculadora de división larga de polinomios se utiliza para dividir funciones polinómicas tomando el divisor y el dividendo. Esta calculadora de división de polinomios encuentra el cociente y resto de las funciones dadas.
¿Qué es la división larga de polinomios?
División larga polinomial es un método Se utiliza para realizar divisiones polinómicas. En este método de división polinomial, el polinomio de mayor grado es el dividendo y el polinomio de menor grado es el divisor.

¿Cómo resolver los problemas de división larga de polinomios?
Los problemas de división larga de polinomios se pueden resolver fácilmente utilizando una calculadora o manualmente. Tomemos un ejemplo para entender este concepto.
Ejemplo
Encuentra la división larga del polinomio si el dividendo del polinomio es 2x 4 + 6x 3 +x 2 + 12x + 20 y el divisor es x+1 .
Solución
Paso 1: Dividimos el término principal del dividendo del polinomio por el término principal del divisor para obtener el primer término del cociente.
2x 4 /x = 2x 3
Esto significa que tienes que multiplicar el divisor por 2x 3 para dar el primer paso.
2x 3 (x+1) = 2x 4 +2x 3
El resto debe ser 4x 3 + x 2 + 12x + 20
Paso 2: Ahora nuevamente divida el término principal del resto del polinomio por el término principal del divisor.
4x 3 /x = 4x 2
Multiplica el divisor por 4 X 2 para dar el segundo paso.
4x 2 (x+1) = 4x 3 +4x 2
El resto debe ser -3x 2 + 12x + 20
Paso 3: Repita los pasos anteriores nuevamente para obtener el tercer resto de la división.
-3x 2 /x = -3x
Multiplica el divisor por -3x para dar el tercer paso.
-3x(x+1) = -3x 2 -3x
El resto debe ser 15x + 20
Etapa 4: Ahora divide el término principal del resto anterior por el primer término del divisor.
15x/x = 15
Multiplica el divisor por 15 para dar el tercer paso.
15(x+1) = 15x + 15
El resto debe ser 5 .
Este es el paso final ya que no queda ninguna variable en el resto de la división.
Por lo tanto
Cociente = 2x 3 + 4x 2 - 3x + 15
Resto = 5
Paso 5: Matemáticamente la división larga del polinomio es: